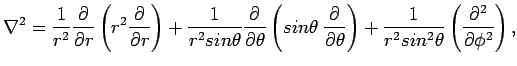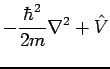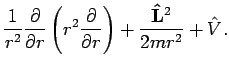Next: About this document ...
Summary of Angular Momentum
We start from the classical expression for angular momentum,
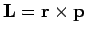 , to obtain the quantum mechanical version
, to obtain the quantum mechanical version
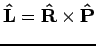 , where
, where 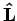 ,
, 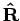 , and
, and 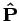 are all three-dimensional vectors. This definition
leads immediately to expressions for the three components of
are all three-dimensional vectors. This definition
leads immediately to expressions for the three components of 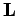 :
:
From these definitions, we may easily derive the following commutators
where the indices 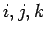 can be
can be 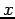 ,
, 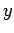 , or
, or 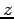 , and where the coefficient
, and where the coefficient
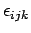 is unity if
is unity if 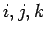 form a cyclic permutation of
form a cyclic permutation of 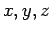 [i.e., (
[i.e., (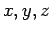 ), (
), (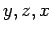 ), or (
), or (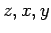 )] and -1 for a reverse
cyclic permutation [(
)] and -1 for a reverse
cyclic permutation [(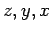 ), (
), (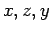 ), or (
), or (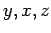 )]. The final
commutator indicates that we cannot generally know
)]. The final
commutator indicates that we cannot generally know 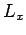 ,
, 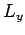 , and
, and 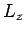 simultaneously except if we have an eigenstate with eigenvalue 0 for each
of these.
simultaneously except if we have an eigenstate with eigenvalue 0 for each
of these.
Classically, any component of the angular momentum must be less than or
equal to the
magnitude of the overall angular momentum vector. Quantum mechanically,
the average value of any component of the angular momentum must be
less than or equal to the square root of the expectation value of 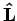 dotted with itself:
dotted with itself:
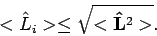 |
(7) |
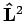 is simply
is simply
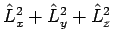 .
.
Since 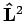 commutes with any component
commutes with any component 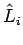 , we can have simultaneous eigenfunctions of
, we can have simultaneous eigenfunctions of 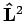 and a given component
and a given component
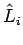 . We usually pick the
. We usually pick the 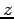 axis, since the expression for
axis, since the expression for 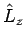 is the easiest of the three when we work in spherical polar
coordinates:
is the easiest of the three when we work in spherical polar
coordinates:
Of course it is also possible to express 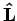 in terms of the unit
vectors for spherical polar coordinates,
in terms of the unit
vectors for spherical polar coordinates,
Here,
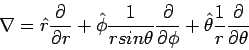 |
(14) |
and
The simultaneous eigenfunctions of 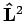 and
and 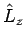 are
called the spherical harmonics,
are
called the spherical harmonics,
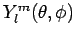 , where
, where 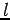 is the total angular momentum quantum number, and
is the total angular momentum quantum number, and 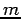 is the so-called
magnetic quantum number. The spherical harmonics are defined as
is the so-called
magnetic quantum number. The spherical harmonics are defined as
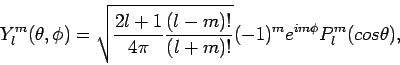 |
(16) |
where 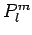 are the associated Legendre polynomials. We require
that
are the associated Legendre polynomials. We require
that
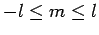 , and spherical harmonics with
, and spherical harmonics with 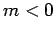 are defined in
terms of the spherical harmonics with
are defined in
terms of the spherical harmonics with 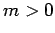 according to
according to
![$Y_l^m = (-1)^m [
Y_l^{-m}]^*$](img61.png) . The spherical harmonics are normalized over integration of
angular coordinates such that
. The spherical harmonics are normalized over integration of
angular coordinates such that
![\begin{displaymath}
\int_0^{\pi} sin \theta \hspace{0.1cm} d\theta \int_0^{2 \pi...
... \phi)]^* Y_l^m(\theta, \phi) =
\delta_{l,l'} \delta_{m, m'},
\end{displaymath}](img62.png) |
(17) |
and they have the following special
properties:
It can be useful to define ladder operators for angular momentum. The
following ladder operators work not only for straight angular momentum 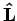 , but also for combined angular momenta such as
, but also for combined angular momenta such as
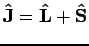 . If
. If
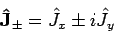 |
(20) |
then
![\begin{displaymath}
{\bf\hat J}_{\pm} \vert jm \rangle =
\hbar \left[ (j \mp m)(j \pm m + 1) \right]^{1/2} \vert j, m \pm 1 \rangle .
\end{displaymath}](img69.png) |
(21) |
We can see that these ladder operators raise or lower the magnetic quantum
number 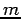 but leave
but leave 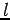 alone.
alone.
One can also show that in spherical polar coordinates
![\begin{displaymath}
{\bf\hat L}^2 = - \hbar^2 \left[
\frac{1}{sin^2 \theta} \fr...
...pace{0.1cm} \frac{\partial}{\partial \theta}
\right) \right].
\end{displaymath}](img70.png) |
(22) |
By comparing this expression with that for 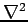 in spherical polar
coordinates,
in spherical polar
coordinates,
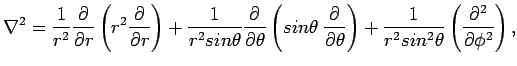 |
|
|
(23) |
we can see that the Hamiltonian can be written as
Clearly 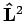 commutes with the kinetic energy term,
commutes with the kinetic energy term, 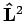 has no
has no 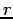 dependence. Likewise, if
dependence. Likewise, if
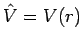 , then
, then 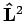 commutes with the whole Hamiltonian. Hence, for problems where
the potential depends only on
commutes with the whole Hamiltonian. Hence, for problems where
the potential depends only on 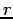 (central force problems), we can find
simultaneous eigenfunctions of
(central force problems), we can find
simultaneous eigenfunctions of 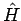 ,
, 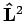 , and
, and 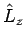 .
.



Next: About this document ...
David Sherrill
2006-02-23
![]() , to obtain the quantum mechanical version
, to obtain the quantum mechanical version
![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are all three-dimensional vectors. This definition
leads immediately to expressions for the three components of
are all three-dimensional vectors. This definition
leads immediately to expressions for the three components of ![]() :
:
![]() dotted with itself:
dotted with itself:
![]() commutes with any component
commutes with any component ![]() , we can have simultaneous eigenfunctions of
, we can have simultaneous eigenfunctions of ![]() and a given component
and a given component
![]() . We usually pick the
. We usually pick the ![]() axis, since the expression for
axis, since the expression for ![]() is the easiest of the three when we work in spherical polar
coordinates:
is the easiest of the three when we work in spherical polar
coordinates:
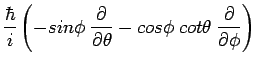
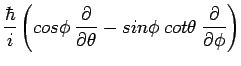
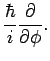
![]() in terms of the unit
vectors for spherical polar coordinates,
in terms of the unit
vectors for spherical polar coordinates,
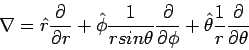
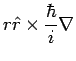
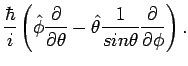
![]() and
and ![]() are
called the spherical harmonics,
are
called the spherical harmonics,
![]() , where
, where ![]() is the total angular momentum quantum number, and
is the total angular momentum quantum number, and ![]() is the so-called
magnetic quantum number. The spherical harmonics are defined as
is the so-called
magnetic quantum number. The spherical harmonics are defined as
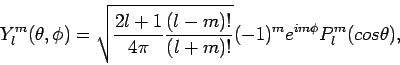
![]() , but also for combined angular momenta such as
, but also for combined angular momenta such as
![]() . If
. If
![\begin{displaymath}
{\bf\hat L}^2 = - \hbar^2 \left[
\frac{1}{sin^2 \theta} \fr...
...pace{0.1cm} \frac{\partial}{\partial \theta}
\right) \right].
\end{displaymath}](img70.png)